TD - Pebble Chess
IPrésentation du jeu
Le but de l'exercice est d'étudier avec des outils mathématiques, un jeu de dame légèrement modifié qui se joue seul, et dont nous présentons les règles :
| Au départ, il y a un damier, des pions placés dans une zone "prison". | Le but est de libérer tous les pions de la zone prison (de nouveaux pions peuvent apparaître). |

|

|
| - Le déplacement des pions est particulier : lorsqu'un pion est déplacé, il se dédouble en créant un pion à sa droite et un pion en dessous de sa position de départ. Il n'est pas possible de réculer et on ne peut pas 'sauter' par dessus un autre pion. | |

|

|
Avant de commencer les maths, essayez différentes stratégies au crayon, en utilisant les cases d'une feuille quadrillée. Une version jouable sur windows est disponible
ici
.
IIMise en place d'un problème mathématique
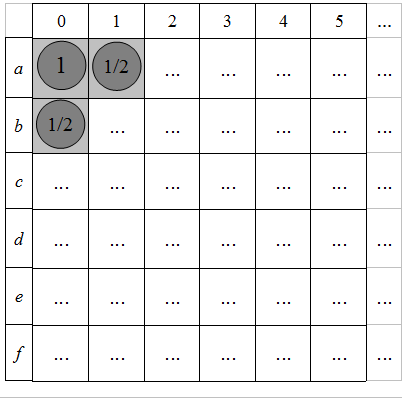
Afin d'étudier mathématiquement ce jeu, nous attribuons un poids à chacun des pions. A chaque fois qu'un pion est déplacé, le poids est divisé en deux et réparti dans les deux pions créés.
Par exemple, si on déplace un pion qui pèse \(1\), les deux pions crées pèseront \(\frac{1}{2}\)et ainsi de suite :

|

|

|
IIIRésolution du problème - Exercice
En fait, il est vain de s'entêter trop longtemps à jouer à ce jeu car, avec cette situation de départ (3 pions dans la prison), il est impossible de gagner. Le but de cet exercice est de le prouver.
1
Justifier qu'à n'importe quel tour de jeu, le poids cumulé des pions présents sur le damier vaut 2.
2
Placer sur chaque case du damier ci-dessous le poids que devrait avoir un pion sur celle-ci.
3
On suppose un damier infini à droite et vers le bas. On définit \((a_n)\) la suite des poids que peut accueillir chaque case sur la ligne \(a\) : \(a_0 = 1, a_1 = 2,\) etc.
a
Quelle est la nature de la suite \((a_n)\) ?
b
On place 5 pions sur les premières cases de la ligne \(a\). Calculer le poids cumulé sur la ligne.
c
Justifier que pour les \(n\) premiers pions, le poids cumulé vaut \(2 (1 - \frac{1}{2^{n}})\)
d
Quelle est le poids limite que peut accueillir la ligne \(a\) ? (réponse sous forme d'une limite)
4
Les lignes suivantes sont assez similaires à la première.
a
Justifier que le poids limite que peut accueillir la ligne \(b\) vaut 1.
b
Quels sont les poids limites que peuvent accueillir les lignes \(c\), \(d\), \(e\) et \(f\) ? Compléter la figure
5
On pose \((p_n)\) la suite des poids limites de chaque ligne : \(p_0\) est le poids de la ligne \(a\), \(p_1\) celui de la ligne \(b\), etc.
a
Quelle est la nature de la suite \((p_n)\) ?
b
Justifier que les \(n\) premières lignes peuvent accueillir ensemble un poids limite de \(4 - \frac{1}{2^{n}}\).
c
En déduire le poids limite que peut accueillir le damier entier.
6
On admet ici que le damier peut accueillir un poids limite de \(4\).
a
Quel poids limite peuvent accueillir la zone prison, et la zone libre ?
b
Pourquoi est-il impossible de gagner ?
c
La conclusion reste-t-elle la même pour toute situatuin de départ ? Justifier.